Parallel-transport and geodesics
Here is an excerpt from the GR lecture notes.
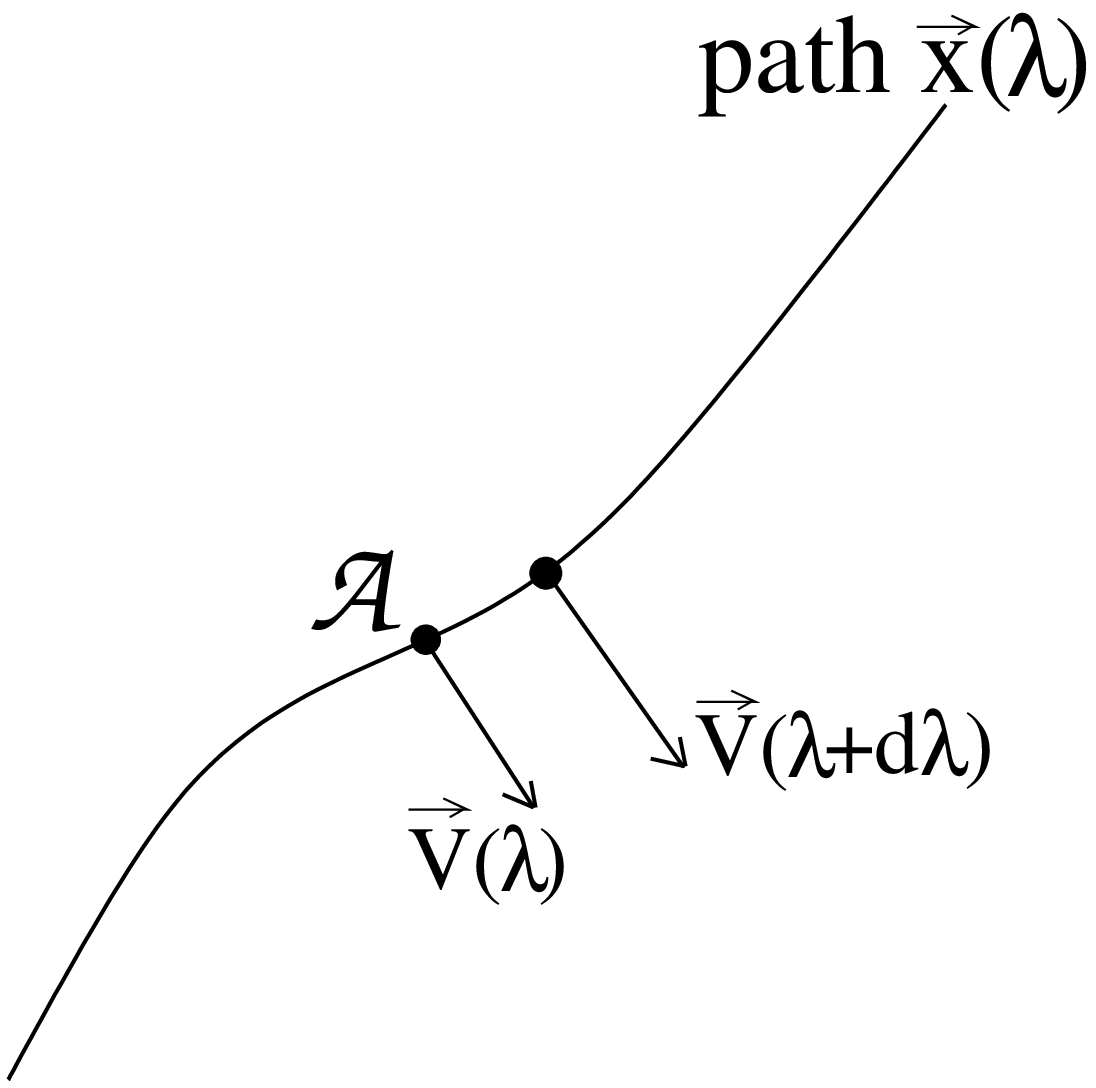
We can use the idea of parallel transport to construct geodesics, defined as curves that parallel-transport their own tangent vectors. That is, for a geodesic
\[ \begin{aligned} \pmb{\nabla}_{\vec u} {\vec u} &= 0 \\ \text{i.e.} \qquad u^\beta {u^\alpha}_{;\beta} &= 0 \\ \text{i.e.} \qquad u^\beta {u^\alpha}_{,\beta} + {\Gamma^\alpha}_{\beta\gamma} u^\beta u^\gamma &= 0 \\ \text{or} \qquad \frac{d}{d\lambda} \left( \frac{d x^\alpha}{d\lambda} \right) + {\Gamma^\alpha}_{\beta\gamma} \frac{d x^\beta}{d\lambda} \frac{d x^\gamma}{d\lambda} &= 0 \end{aligned} \]
where in the last of these expressions (often called the geodesic equation, though the first is also the geodesic equation), \(\lambda\) is a continuous parameter along the curve.
We have some freedom to choose \(\lambda\) – if we choose it to be the proper time of a particle with the curve as its world line, then \(\vec{u}\) is the velocity of the particle. However, \(\lambda\) is a more general quantity and can be used also for light rays with no proper time. Any linear transformation of \(\lambda\), such as \(\phi = a \lambda + b\) with \(a\), \(b\) constants, has \(\vec{x}(\phi)\) a valid solution of the geodesic equation (try the transformation \(\lambda \to \phi\)) – we refer to \(\lambda\) (or \(\phi\)) as an affine parameter.
In a locally-flat region, where the Christoffel symbols vanish, clearly the geodesic equation reduces to
\[ \frac{d^2 x^\alpha}{d\lambda^2} = 0 \]
which solves to the straight-line solution
\[ x^\alpha = A^\alpha \lambda + B^\alpha. \]
In fact we can say, in a very real sense, that all geodesics are straight. This definition about “parallel transport of the tangent vector” is the only sensible definition of a straight line – it means that the curve at each point keeps moving in the direction of its local tangent vector. No other frame-independent definition of “straight” makes sense.